Priority queue

In computer science, a priority queue is an abstract data type which is like a regular queue or stack data structure, but additionally, each element is associated with a "priority".

stack — elements are pulled in last-in first-out-order (e.g. a stack of papers)
queue — elements are pulled in first-in first-out-order (e.g. a line in a cafeteria)
priority queue — elements are pulled highest-priority-first (e.g. cutting in line, or VIP service).

It is a common misconception that a priority queue is a heap. A priority queue is an abstract concept like "a list" or "a map"; just as a list can be implemented with a linked list or an array, a priority queue can be implemented with a heap or a variety of other methods.

A priority queue must at least support the following operations:

insert_with_priority: add an element to the queue with an associated priority
pull_highest_priority_element: remove the element from the queue that has the highest priority, and return it (also known as "pop_element(Off)", "get_maximum_element", or "get_front(most)_element"; some conventions consider lower priorities to be higher, so this may also be known as "get_minimum_element", and is often referred to as "get-min" in the literature; the literature also sometimes implement separate "peek_at_highest_priority_element" and "delete_element" functions, which can be combined to produce "pull_highest_priority_element")

More advanced implementations may support more complicated operations, such as pull_lowest_priority_element, inspecting the first few highest- or lowest-priority elements (peeking at the highest priority element can be made O(1) time in nearly all implementations), clearing the queue, clearing subsets of the queue, performing a batch insert, merging two or more queues into one, incrementing priority of any element, etc.

1 Similarity to queues
2 Implementation
3 Equivalence of priority queues and sorting algorithms
- 3.1 Using a priority queue to sort
- 3.2 Using a sorting algorithm to make a priority queue
4 Libraries
5 Applications
6 See also
7 References
8 Further reading
9 External links

Similarity to queues

One can imagine a priority queue as a modified queue, but when one would get the next element off the queue, the highest-priority element is retrieved first.

Stacks and queues may be modeled as particular kinds of priority queues. In a stack, the priority of each inserted element is monotonically increasing; thus, the last element inserted is always the first retrieved. In a queue, the priority of each inserted element is monotonically decreasing; thus, the first element inserted is always the first retrieved.

Implementation

Naive implementations

There are a variety of simple, usually inefficient, ways to implement a priority queue. They provide an analogy to help one understand what a priority queue is. For instance, one can keep all the elements in an unsorted list. Whenever the highest-priority element is requested, search through all elements for the one with the highest priority. (O(1) insertion time, O(n) pull time due to search)

Usual implementation

To get better performance, priority queues typically use a heap as their backbone, giving O(log n) performance for inserts and removals, and O(n) to build initially. Alternatively, if a self-balancing binary search tree is used, insertion and removal also take O(log n) time, although building the tree from an existing sequence of elements takes O(n log n) time; this is a popular solution where one already has access to these data structures, such as through third-party or standard libraries.

Note that from a computational-complexity standpoint, priority queues are equivalent to sorting algorithms. See the next section for how efficient sorting algorithms can create efficient priority queues.

Effect of different data structures

The designer of the priority queue should take into account what sort of access pattern the priority queue will be subject to, and what computational resources are most important to the designer. The designer can then use various specialized types of heaps:

There are a number of specialized heap data structures that either supply additional operations or outperform the above approaches. The binary heap uses O(log n) time for both operations, but allows peeking at the element of highest priority without removing it in constant time. Binomial heaps add several more operations, but require O(log n) time for peeking. Fibonacci heaps can insert elements, peek at the highest priority element, and increase an element's priority in amortized constant time (deletions are still O(log n)).

While relying on a heap is a common way to implement priority queues, for integer data faster implementations exist (this can even apply to datatypes that have finite range, such as floats):

When the set of keys is {1, 2, ..., C}, a van Emde Boas tree supports the minimum, maximum, insert, delete, search, extract-min, extract-max, predecessor and successor operations in 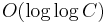$O(\log \log C)$ time, but has a space cost for small queues of about O(2^m/2), where m is the number of bits in the priority value.^[1]
The Fusion tree algorithm by Fredman and Willard implements the minimum operation in O(1) time and insert and extract-min operations in 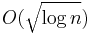$O(\sqrt{\log n})$ time.^[2]

For applications that do many "peek" operations for every "extract-min" operation, the time complexity for peek can be reduced to O(1) in all tree and heap implementations by caching the highest priority element after every insertion and removal. (For insertion this adds at most constant cost, since the newly inserted element need only be compared to the previously cached minimum element. For deletion, this at most adds an additional "peek" cost, which is nearly always cheaper than the deletion cost, so overall time complexity is not affected by this change).

Equivalence of priority queues and sorting algorithms

Using a priority queue to sort

The semantics of priority queues naturally suggest a sorting method: insert all the elements to be sorted into a priority queue, and sequentially remove them; they will come out in sorted order. This is actually the procedure used by several sorting algorithms, once the layer of abstraction provided by the priority queue is removed. This sorting method is equivalent to the following sorting algorithms:

Heapsort if the priority queue is implemented with a heap.
Smoothsort if the priority queue is implemented with a Leonardo heap.
Selection sort if the priority queue is implemented with an unordered array.
Insertion sort if the priority queue is implemented with an ordered array.
Tree sort if the priority queue is implemented with a self-balancing binary search tree.

Using a sorting algorithm to make a priority queue

A sorting algorithm can also be used to implement a priority queue. Specifically, Thorup says^[3]:

We present a general deterministic linear space reduction from priority queues to sorting implying that if we can sort up to n keys in S(n) time per key, then there is a priority queue supporting delete and insert in O(S(n)) time and find-min in constant time.

That is, if there is a sorting algorithm which can sort in O(S) time per key, where S is some function of n and word size ^[4], then one can use the given procedure to create a priority queue where pulling the highest-priority element is O(1) time, and inserting new elements (and deleting elements) is O(S) time. For example if one has an O(n lg(lg(n))) sort algorithm, one can easily create a priority queue with O(1) pulling and O(lg(lg(n))) insertion.

Libraries

A priority queue is often considered to be a "container data structure".

The Standard Template Library (STL), and the C++ 1998 standard, specifies priority_queue as one of the STL container adaptor class templates. It implements a max-priority-queue. Unlike actual STL containers, it does not allow iteration of its elements (it strictly adheres to its abstract data type definition). STL also has utility functions for manipulating another random-access container as a binary max-heap.

Python's heapq module implements a binary min-heap on top of a list.

Java's library contains a PriorityQueue class, which implements a min-priority-queue.

Go's library contains a container/heap module, which implements a min-heap on top of any compatible data structure.

The Standard PHP Library extension contains the class SplPriorityQueue.

Apple's Core Foundation framework contains a CFBinaryHeap structure, which implements a min-heap.

Applications

Bandwidth management

Priority queuing can be used to manage limited resources such as bandwidth on a transmission line from a network router. In the event of outgoing traffic queuing due to insufficient bandwidth, all other queues can be halted to send the traffic from the highest priority queue upon arrival. This ensures that the prioritized traffic (such as real-time traffic, e.g. an RTP stream of a VoIP connection) is forwarded with the least delay and the least likelihood of being rejected due to a queue reaching its maximum capacity. All other traffic can be handled when the highest priority queue is empty. Another approach used is to send disproportionately more traffic from higher priority queues.

Many modern protocols for Local Area Networks also include the concept of Priority Queues at the Media Access Control (MAC) sub-layer to ensure that high-priority applications (such as VoIP or IPTV) experience lower latency than other applications which can be served with Best effort service. Examples include IEEE 802.11e (an amendment to IEEE 802.11 which provides Quality of Service) and ITU-T G.hn (a standard for high-speed Local area network using existing home wiring (power lines, phone lines and coaxial cables).

Usually a limitation (policer) is set to limit the bandwidth that traffic from the highest priority queue can take, in order to prevent high priority packets from choking off all other traffic. This limit is usually never reached due to high level control instances such as the Cisco Callmanager, which can be programmed to inhibit calls which would exceed the programmed bandwidth limit.

Discrete event simulation

Another use of a priority queue is to manage the events in a discrete event simulation. The events are added to the queue with their simulation time used as the priority. The execution of the simulation proceeds by repeatedly pulling the top of the queue and executing the event thereon.

Dijkstra's algorithm

When the graph is stored in the form of adjacency list or matrix, priority queue can be used to extract minimum efficiently when implementing Dijkstra's algorithm.

A* and SMA* search algorithms

The A* search algorithm finds the shortest path between two vertices or nodes of a weighted graph, trying out the most promising routes first. The priority queue (also known as the fringe) is used to keep track of unexplored routes; the one for which a lower bound on the total path length is smallest is given highest priority. If memory limitations make A* impractical, the SMA* algorithm can be used instead, with a double-ended priority queue to allow removal of low-priority items.

ROAM triangulation algorithm

The Real-time Optimally Adapting Meshes (ROAM) algorithm computes a dynamically changing triangulation of a terrain. It works by splitting triangles where more detail is needed and merging them where less detail is needed. The algorithm assigns each triangle in the terrain a priority, usually related to the error decrease if that triangle would be split. The algorithm uses two priority queues, one for triangles that can be split and another for triangles that can be merged. In each step the triangle from the split queue with the highest priority is split, or the triangle from the merge queue with the lowest priority is merged with its neighbours.

References

^ P. van Emde Boas. Preserving order in a forest in less than logarithmic time. In Proceedings of the 16th Annual Symposium on Foundations of Computer Science, pages 75-84. IEEE Computer Society, 1975.
^ Michael L. Fredman and Dan E. Willard. Surpassing the information theoretic bound with fusion trees. Journal of Computer and System Sciences, 48(3):533-551, 1994
^ Mikkel Thorup. 2007. Equivalence between priority queues and sorting. J. ACM 54, 6, Article 28 (December 2007). DOI=10.1145/1314690.1314692 [1]
^ http://courses.csail.mit.edu/6.851/spring07/scribe/lec17.pdf

External links

C++ reference for std::priority_queue
Descriptions by Lee Killough
PQlib - Open source Priority Queue library for C
libpqueue is a generic priority queue (heap) implementation (in C) used by the Apache HTTP Server project.
Survey of known priority queue structures by Stefan Xenos
UC Berkeley - Computer Science 61B - Lecture 24: Priority Queues (video) - introduction to priority queues using binary heap
Double-Ended Priority Queues by Sartaj Sahni